PUZZLeaTOMictM

EC CURVES DRAWING SYSTEM 

Click here to start the ECCurves creation system. Before starting ECCurves you should first read below to learn how it works.

 A simple ECCurve example. Create a random curve or curves with lines.  Add effects.  Save or print.  Create your own factor pattern.

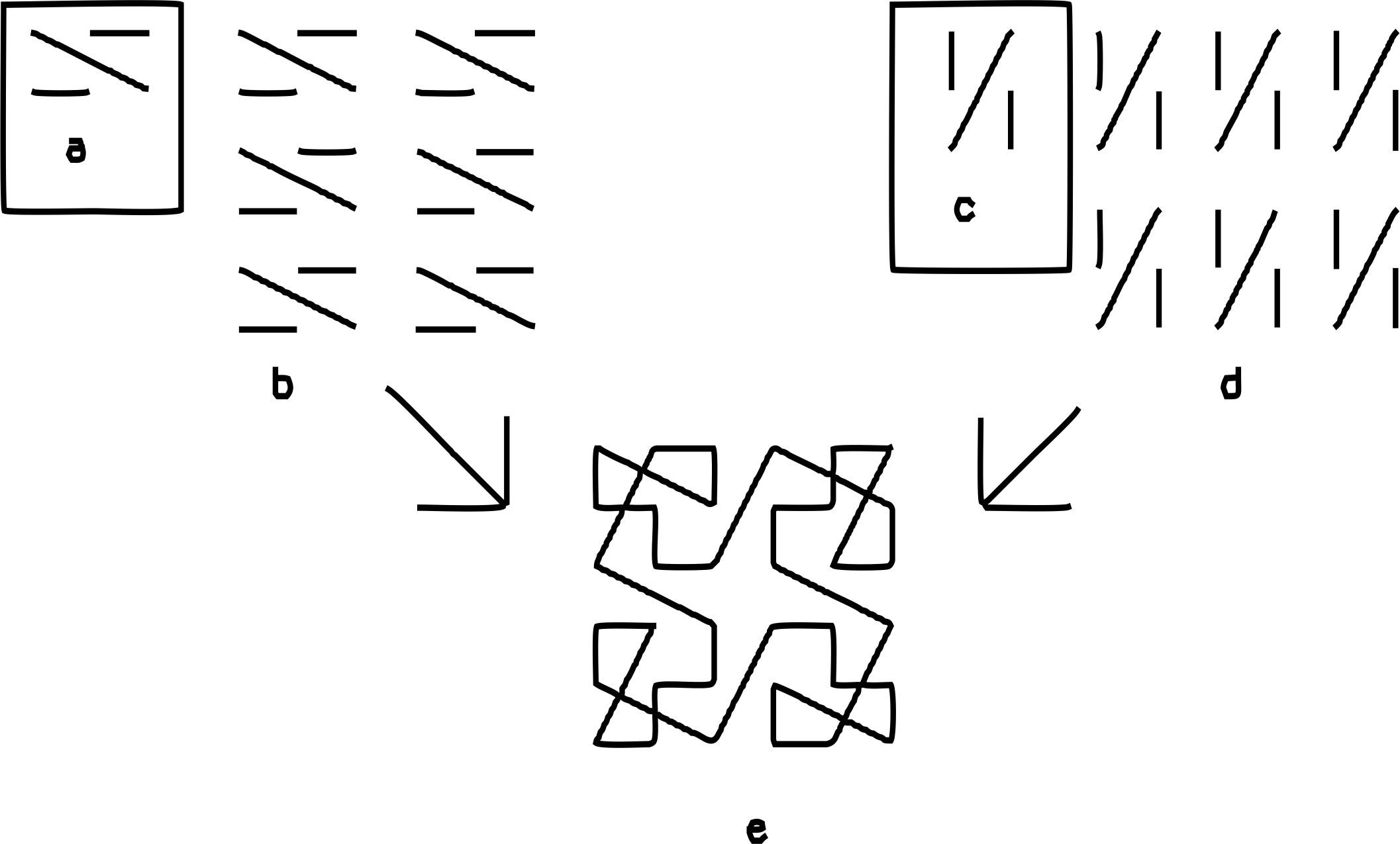
A simple ECCurve example.   To create an ECCurve make a rectangular 2x3 array of points. Connect all the pairs of points in the array with lines, as in a below.  The array shown in a is an m by n array where m=3, n=2. Such a pattern is called is a factor pattern or ECC factor. Repeat the pattern n by m times to create the square pattern as shown in b. Turn the factor pattern 90 degrees as in c and repeat it m by n times to make the pattern shown in d. Finally to make the product pattern you overlap the square pattern in b with the square pattern in d to create the product pattern shown in e. This is the product pattern, axb. The product pattern shown in e is also a Celtic curve(pronounced Keltik), since it forms a single closed circuit. The ancient Celts believed such a closed loop represented life from birth to death. They created amazing and beautiful works of art with closed, knotted loops, on stones, belts, gold work, books, cloth, and other materials.

,

ECCurves(pronounced 'ee see curves') can also be made by multiplying 3D patterns in different ways.  The idea for ECCurve product patterns was published in the problems section of the American Mathematical Monthly, Feb. 1983 Vol 2. Another publication of the idea was in the Journal of Recreational Mathematics V13(1) 1980-81. Later a small self published book was written called Engel Curves (name now changed to ECCurves for Engel Circuit Curves).   'Engel Curves' is no longer printed but may be edited and published in the future with a new title.    Many interesting ECCurve patterns can be found that have a mathematical basis.  However very little of the math has been formalized, as far as the writer knows, making these ECCurves a fertile subject for research and development. 

 Not all ECCurve factor patterns produce closed circuits when multiplied.  This is because a factor pattern consists of pairs of points connected by mn/2 lines(only one line can emanate from each point).  Thus if the square grid of points = mn is odd then at least one point can not have a line going to it.   When this is the case, and the product pattern is formed a given circuit need not be closed but can start at one point and end at another point.  In other cases two points can overlap in the product pattern so that no lines emanate from that point position.

Eccurves are copyrighted as a creative design program and its output.  You may print and use the patterns for your own use.  Any commercial use for profit must give credit to the Eccurves system and Doug Engel.  Commercial use for mass sales requires a royalty agreement that can be obtained from Doug Engel, owner of the system.  The program was developed with the help of my colleague Troy Black who is also an electronics and mechanical whiz.

Create a random curve or curves with lines.

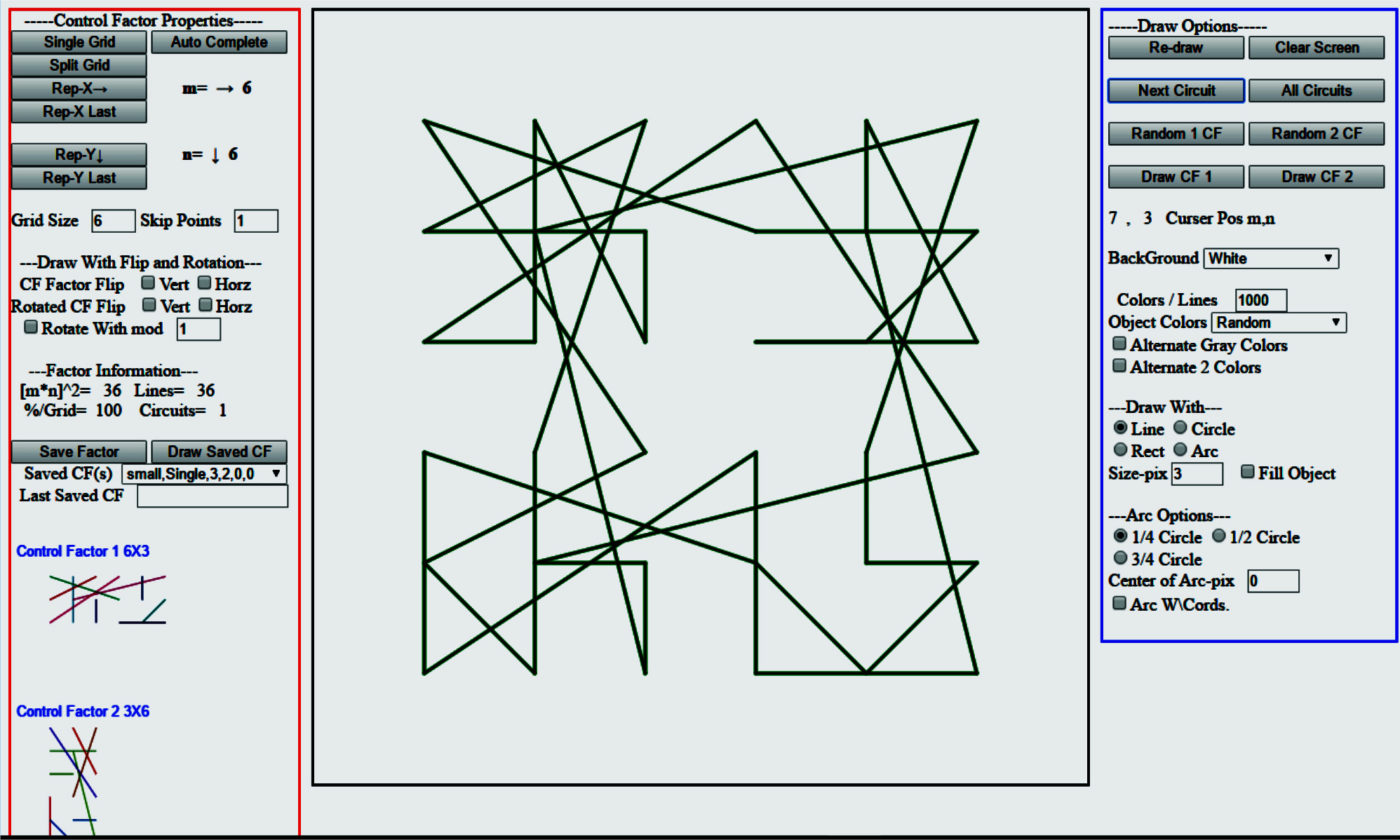
Quick start:  Here is an overview of the program when you first start it up.  Click in  'Grid Size' box (left screen area) and enter 6.  Click on 'Random 1CF' (upper right screen area).  In the example shown here  the 'Random 1CF' draws a 6x3 factor pattern.  You can see the factor pattern and its rotation at the lower left screen area.  Click on 'Background' and set color to White at right screen area.  Click on 'Next Circuit'  (upper right screen area).  This draws the first circuit at center area where the multiplied patterns are drawn.  Click on 'Next Circuit' again to draw the next circuit.  If you want to see all the circuits click on "All circuits".  The left screen area under '--Furthur Information--' shows m*n^2=36 = no. of points in the product pattern, and also shows Lines=36, %Grid=100, Circuits=1.  This is information about the product pattern circuits drawn.  If you see Circuits=1 and %Grid=100 then the product is a single closed loop, a Celtic Curve.  Celtic Curves for random product patterns are uncommon.  Usually several circuits are formed when %Grid=100 but in this case a single circuit 'Celtic Curve was drawn.

Add effects. 

You can change the look of the circuits by clicking on various  option buttons.  In the example below grid size has been set to 4.  At the left Vert factor flip has been chosen.  A random 1 CF button click has drawn the two factor patterns at lower left.  At the right screen background is set to white and object colors to black to draw black lines.  Size of the pixels is set to 3, draw with option has 'Line' selected.  Although Center of arc-pix is set to 20 it has not effect since we are not drawing arcs.  Click 'Next Circuit' to draw the first circuit then click 'All Circuits' to draw all the circuits producing circuits=20 and lines =144.  This factor will be used in several examples to illustrate what different settings in the right and left screen areas does to the same factor pattern.

Add effects continued.

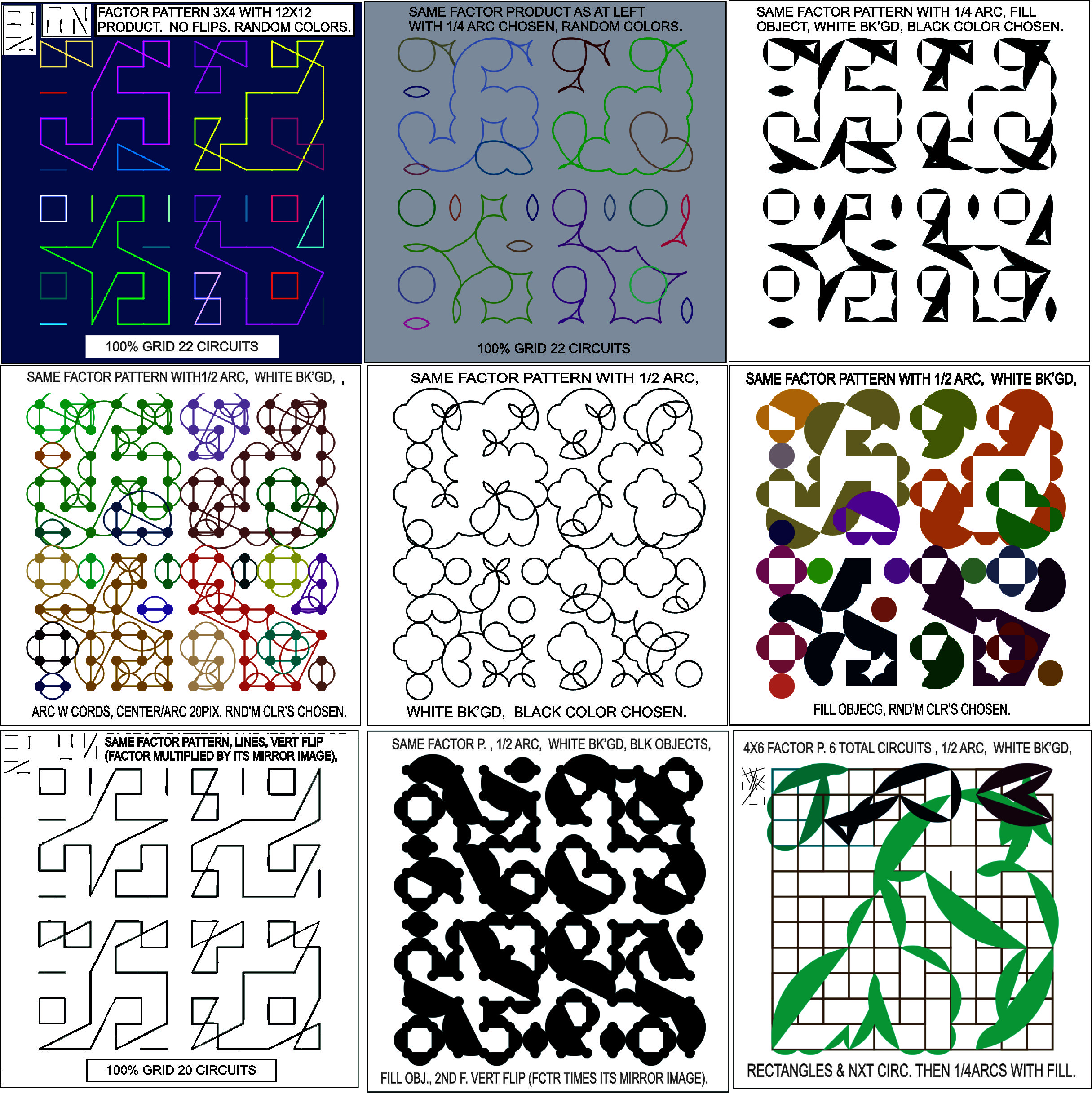
The figure below shows nine different ways to produce the same or similar products with a single starting factor pattern.  These will be referred to as 1 thru 9 numbering left to right.  The first pattern shows the factor patterns at the upper left in white boxes.  It was generated by using the option of random background color and random object colors.  In this case the objects are the circuit lines.  It generated 22 total circuits, 100% of grid points visited by the circuits.  For pattern number two random colors once again but instead of lines the 1/4arc optionn was checked.  While you can see resemblances of the two patterns the artistic effect is very different, almost like going from printed lettering to cursive lettering.  Or going from a disciplined tile look to a free form expressive style.  Number three we chose white background and filled objects, 1/4arcs, and black object colors were chosen.  The fourth pattern used a white background, random objects and 1/2 arcs with chord lines, thus it shows the lines of circuit pattern number 1 plus 1/2 circle lines.  It also drew a 20 pixel dot at each grid point.  Number five pattern also has 1/2 arcs chosen with white and black and no chords or large grid dots.  At number six the 1/2 ars are filled objects with random object colors.  All the products except the last three generated 22 circuits for the filled grid.  For pattern seven, lines are chosen with the additional trick of doing a vertical flip of one of the factors to produce a pattern bilaterally symmetric along a diagonal.  Because one of the patterns has been flipped a different product is produced with 20 circuits.  In number 8 the other factor has been flipped about the vertical axis to produce the filled object product.

Finally for pattern number nine a different factor was used to create the pattern.  First choose rectangles for the objects then click 'draw next circuit' to draw the box like circuit.  Next the 1/4arc option was chosen and the rest of the circuits were generated.  This shows how you can mix all kinds of effects in the same product pattern for a practically unlimited variety of mathematically artistic effects.